dirtsa wrote:
當audio engineering...(恕刪)
dirtsa 宅男工程師 其實這部分我比較難理解的是為何需要找到一個參數去解析音色,
解析他的好處在哪?系統能打的出來不是比較重要?復現的工程上需要這樣反推的實務應用在那?
流程應該是盡可能去確保輸出等於輸入為必要條件,做出一個能接近理想的輸入輸出系統,最後再套上option 用家要的一些filter DSP eq 或是一些人因工程研究後最佳化效果等等濾鏡即可。
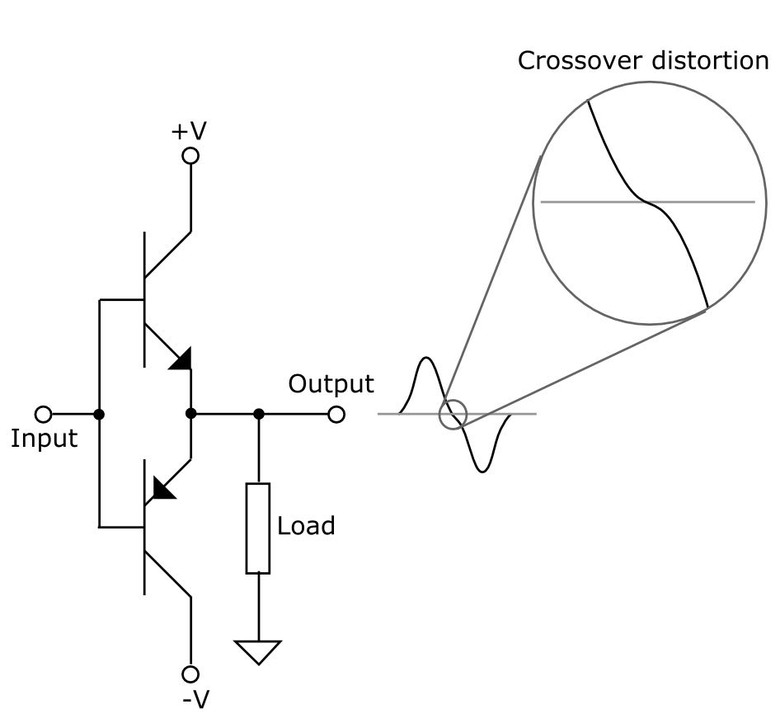
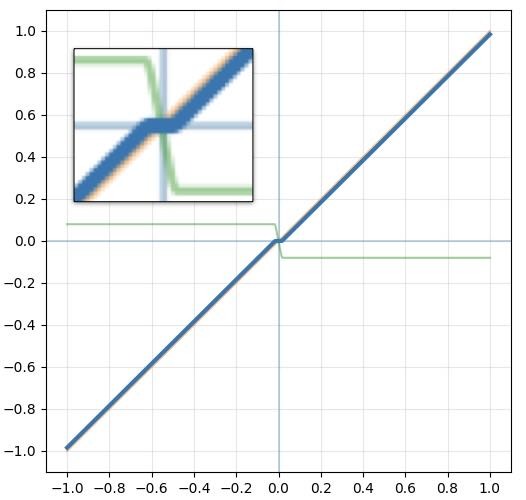
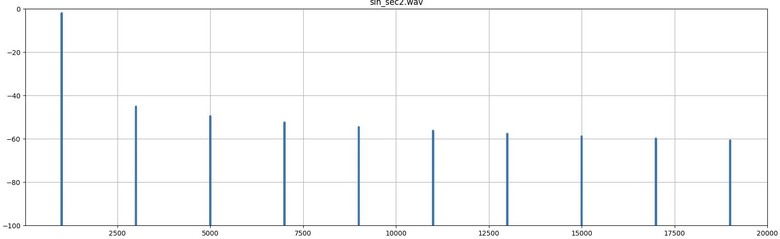

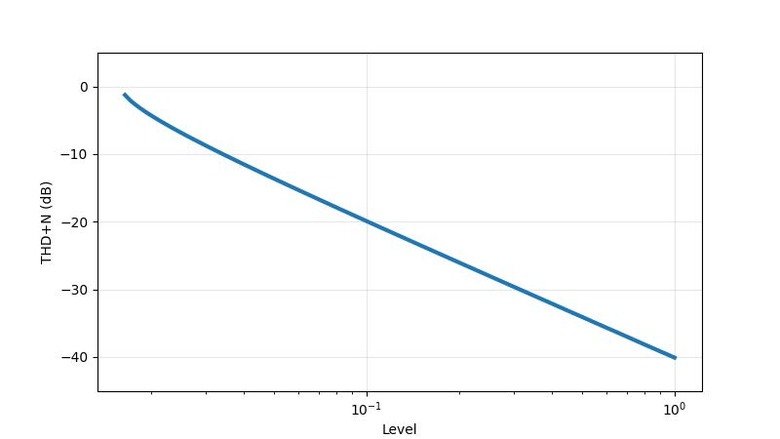
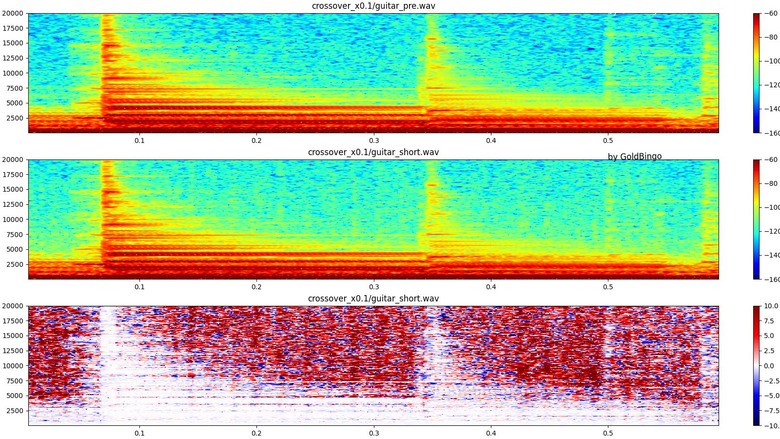
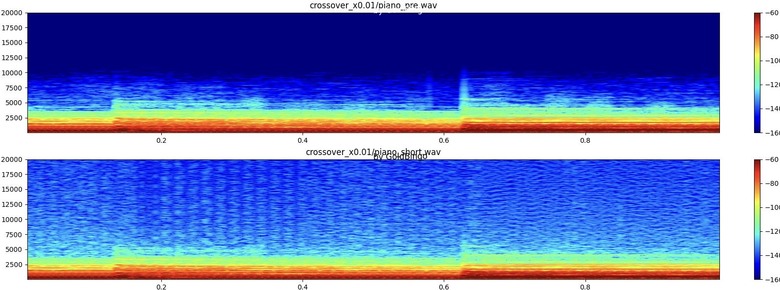
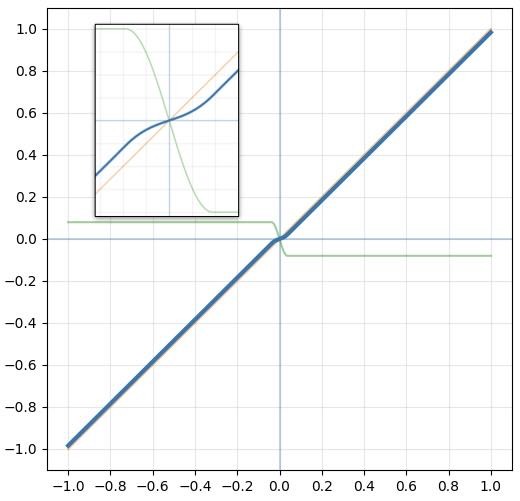
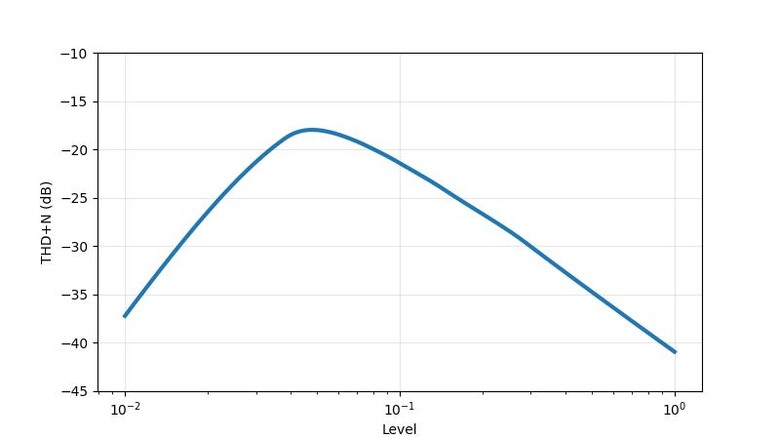
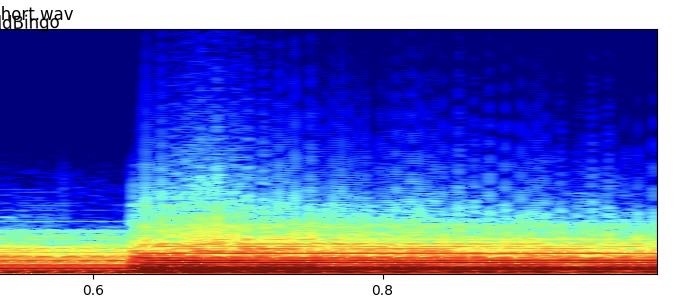
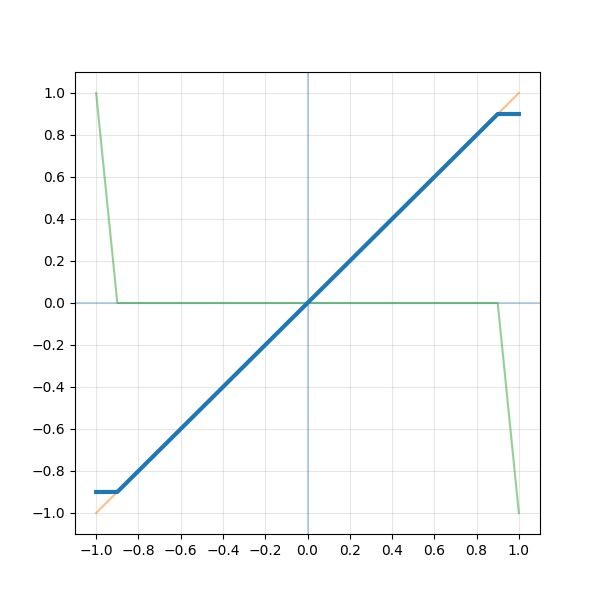
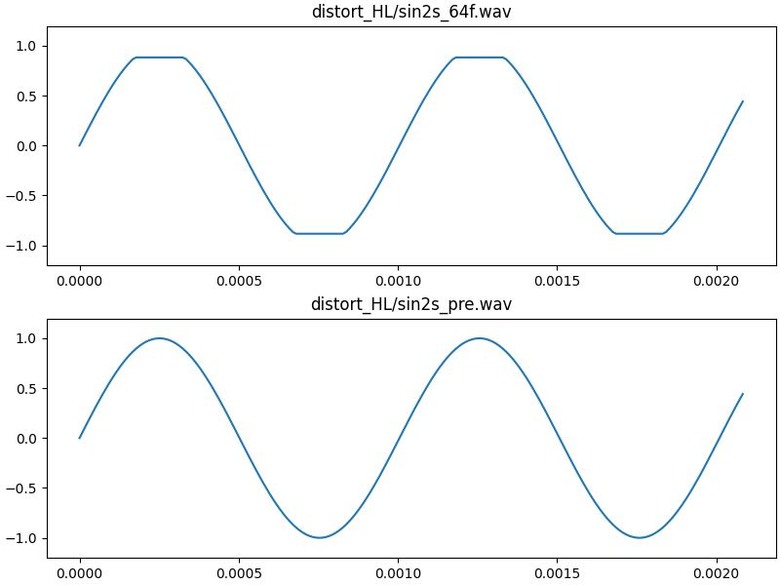

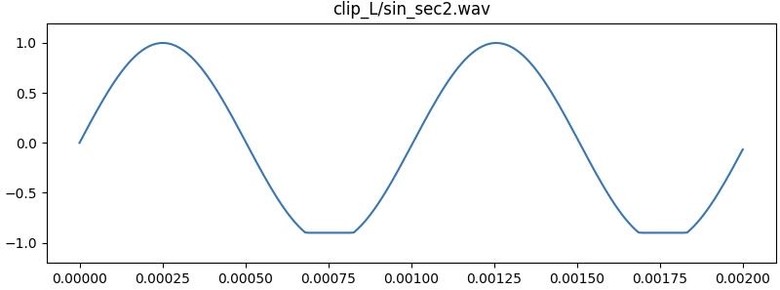

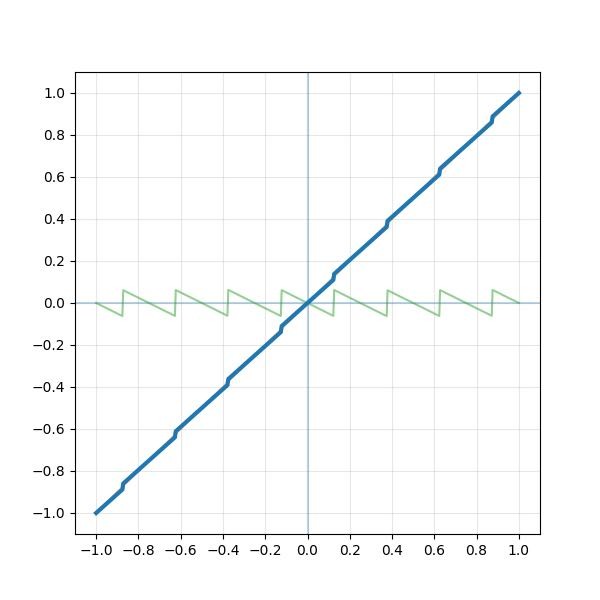
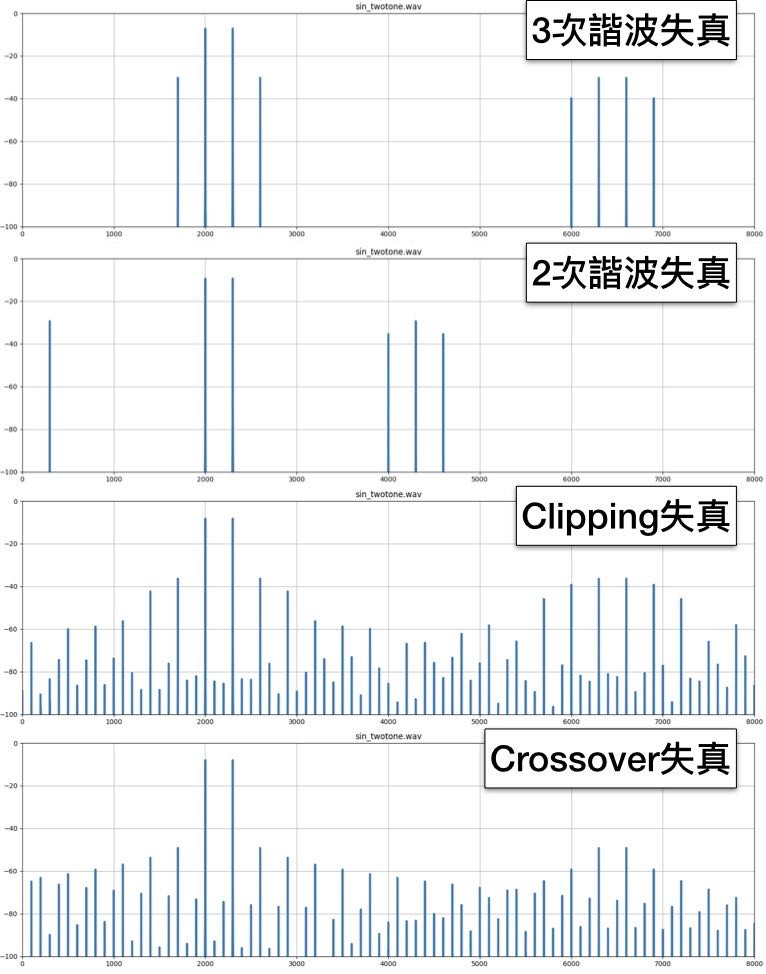
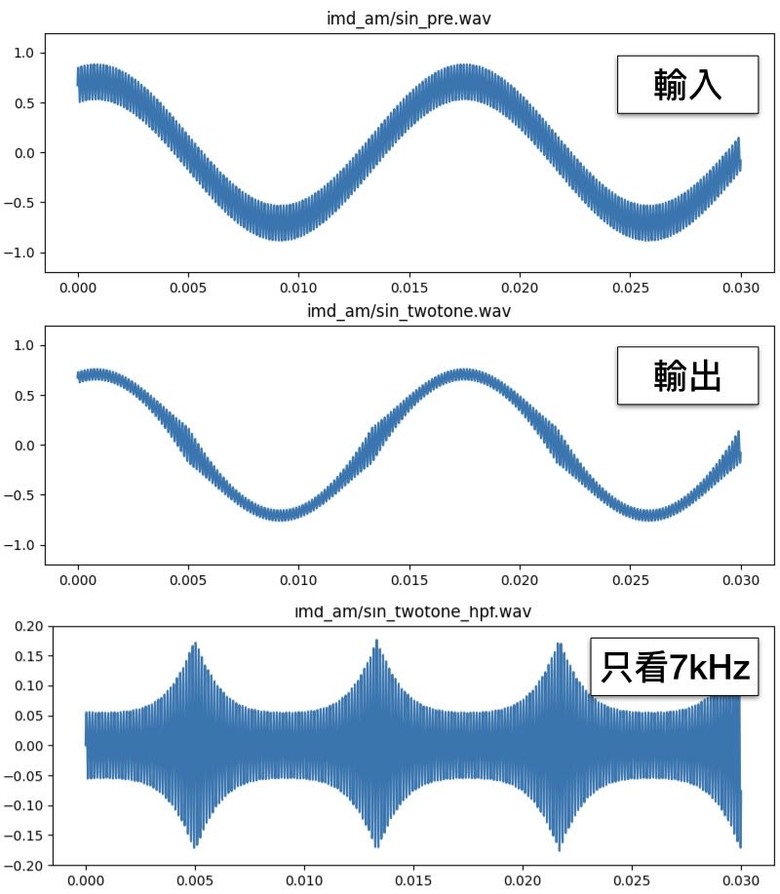
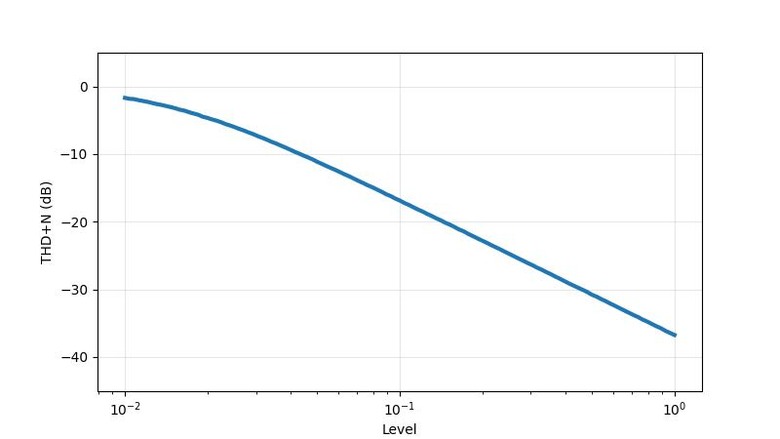
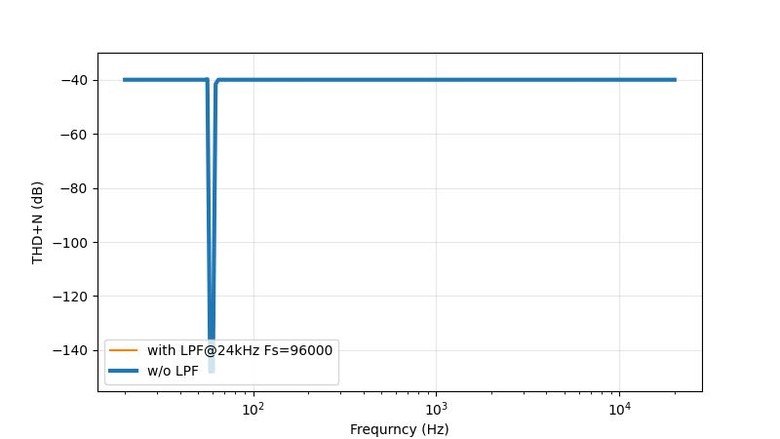
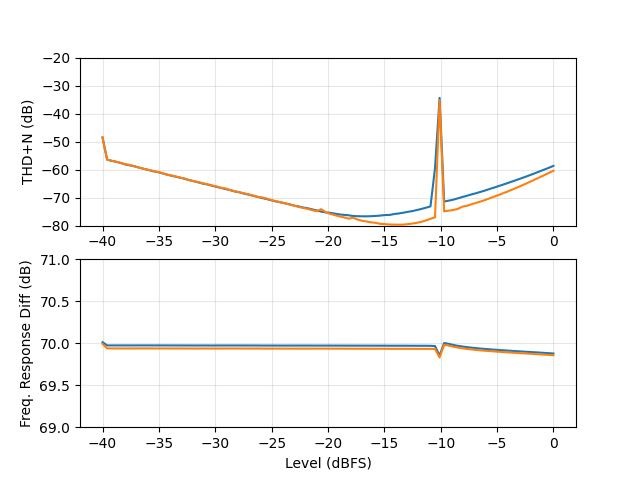
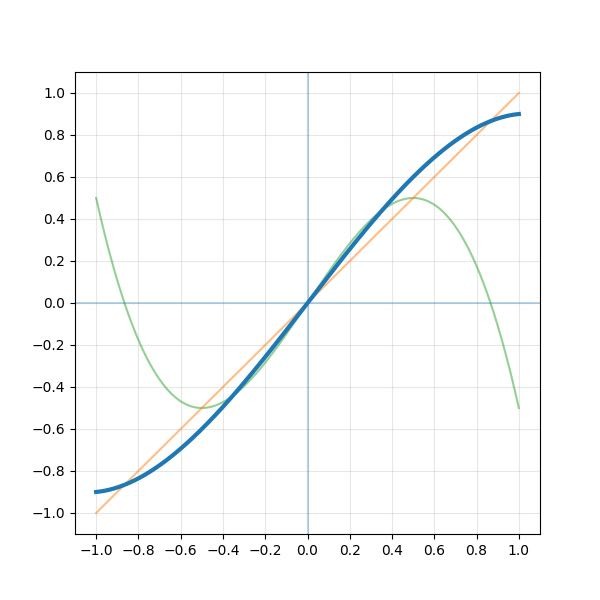
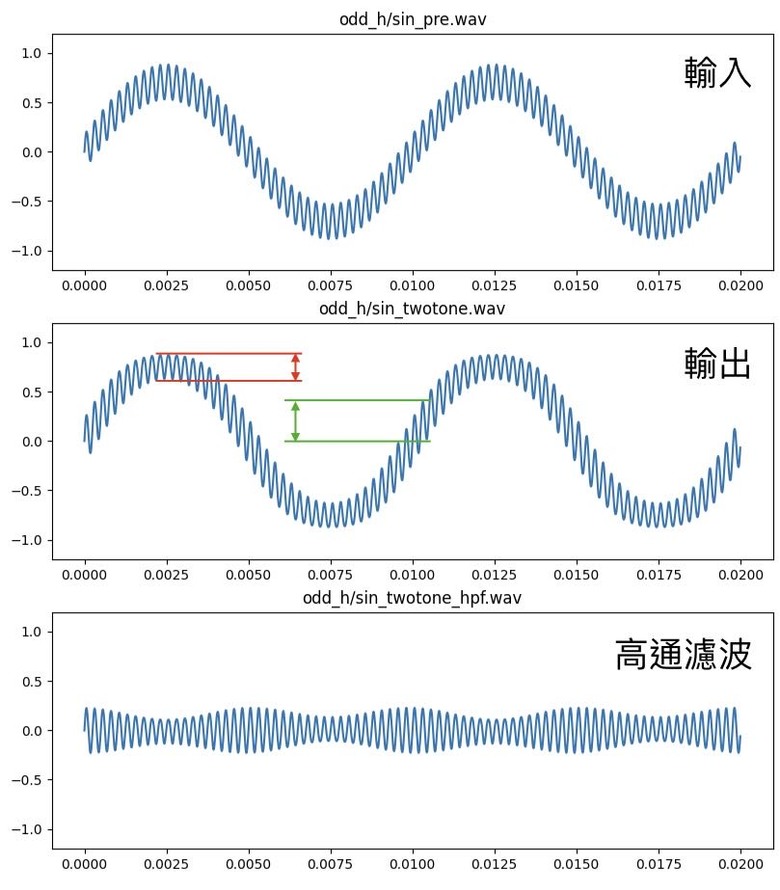
 。以振幅掃THD圖,也可印證此狀況。0.125以下無失真,一超過THD立刻暴升。隨著振幅變大會經過的其他不平滑處,也都會看到對應的起伏點。
。以振幅掃THD圖,也可印證此狀況。0.125以下無失真,一超過THD立刻暴升。隨著振幅變大會經過的其他不平滑處,也都會看到對應的起伏點。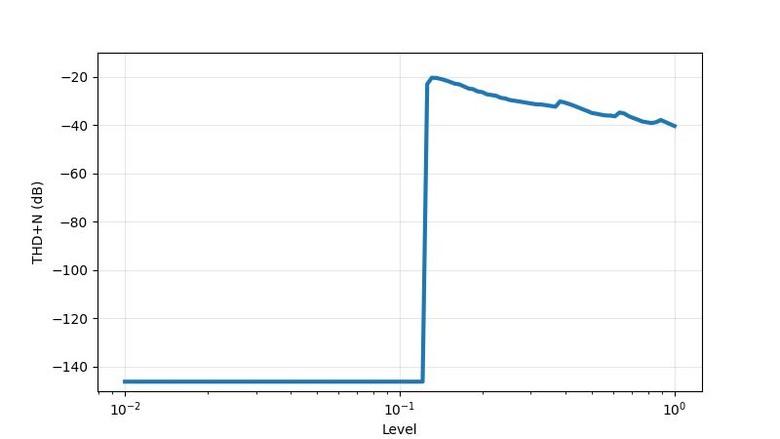
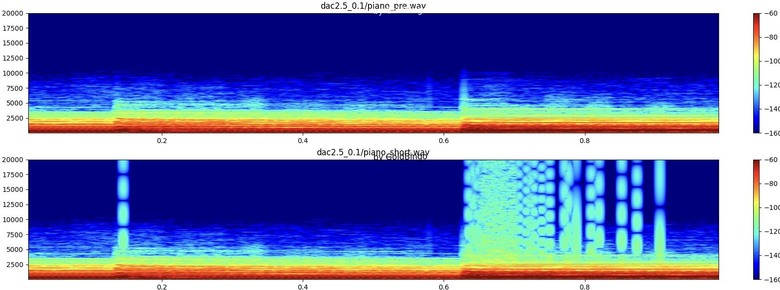
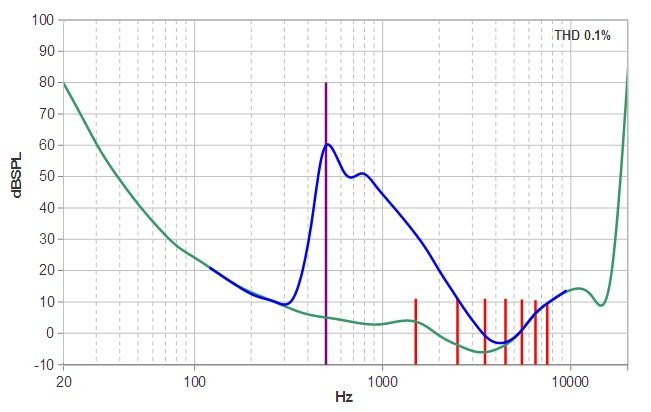
 。在解讀THD數據時,不一定低的,就一定聽起來感覺失真小。
。在解讀THD數據時,不一定低的,就一定聽起來感覺失真小。goldbingo wrote:
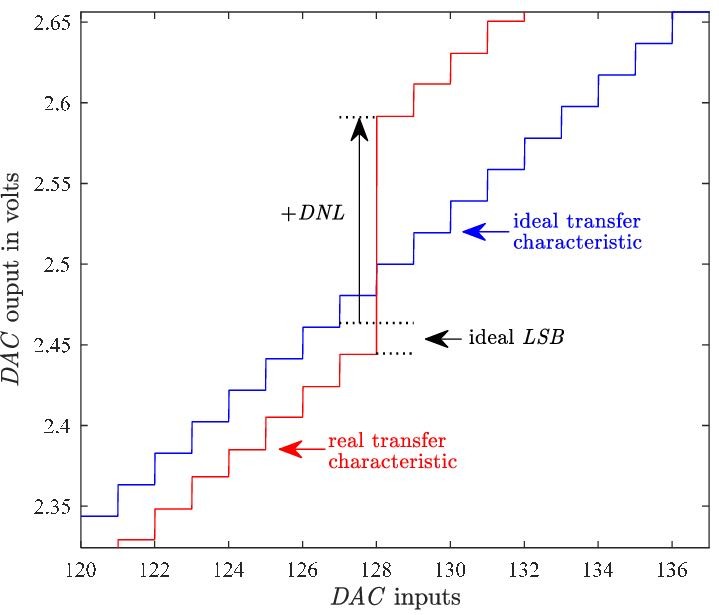
DAC可能因電路設計不理想性,在某些位元轉換處,產生較大的DNL,
在R2R這類很吃元件match特性的DAC尤其挑戰高
goldbingo wrote:
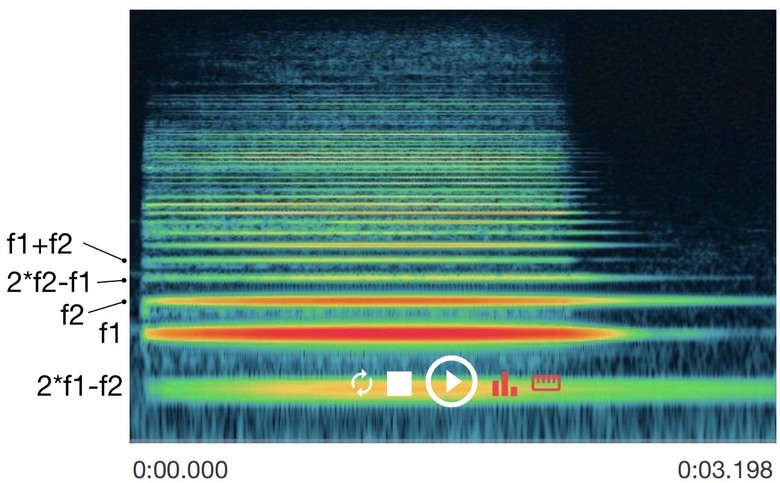
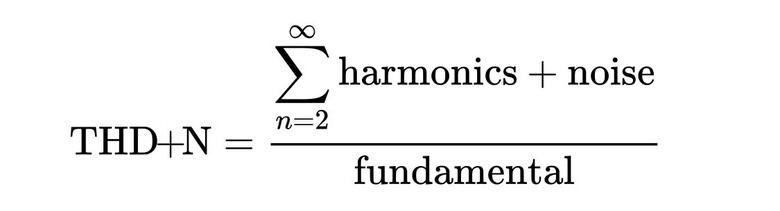
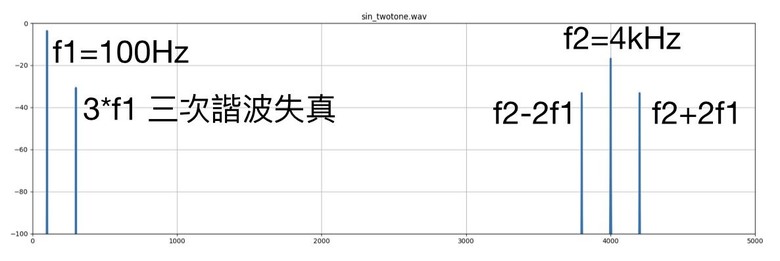
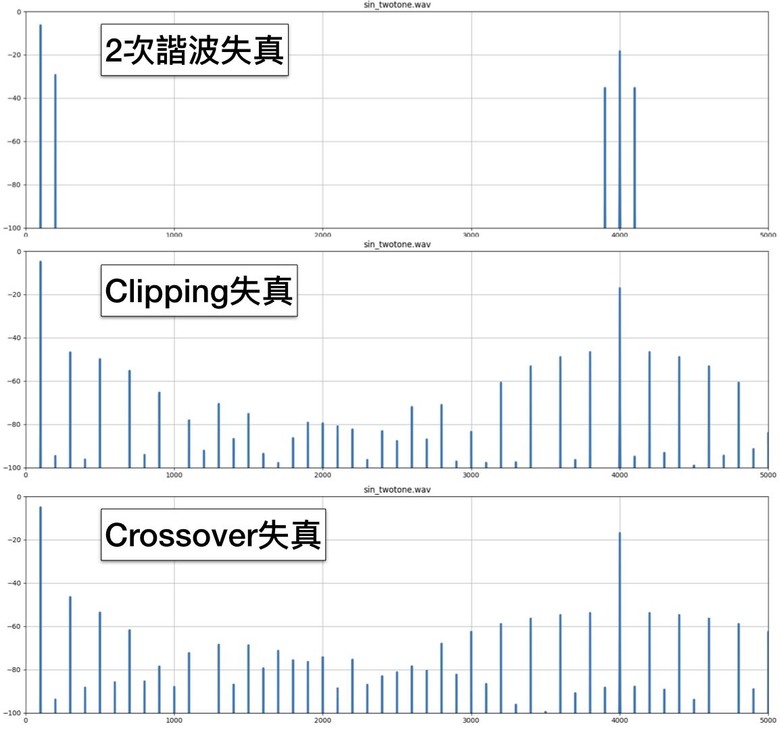
同樣1% THD在不同頻率組成下,聽感感受的失真度卻是天差地遠。
誰阿 wrote:
其實這部分我比較難理解的是為何需要找到一個參數去解析音色
誰阿 wrote:
做出一個能接近理想的輸入輸出系統,最後再套上option ...(恕刪)
 ,調整聽感不影響其技術面失真指標。這樣就不會因量測數據而錯過想要的聲音。
,調整聽感不影響其技術面失真指標。這樣就不會因量測數據而錯過想要的聲音。 。
。



goldbingo wrote:
舉Ayre QB-9的做法為例,它就有點這個味道。這部DAC在後面附上了可以切換
MY-HiEND wrote:
您知道為什麼Ayre 從來不生產分體式的轉盤及DAC 嗎?為什麼QB-9 會成為Ayre 第一台獨立的DAC?今年9 月Ayre 市場經理Brent 來時,我特別問了他這點,答案其實很簡單,關鍵就在於時基誤差(jitter)。標準的S/PDIF(Sony/Philips Digital Interface Format)數位傳輸方式是沒有辦法避免jitter 的產生,這對要求完美的Ayre 來說,是沒有辦法忍受jitter 對聲音所造成的劣化。
 。
。宅男工程師 wrote:
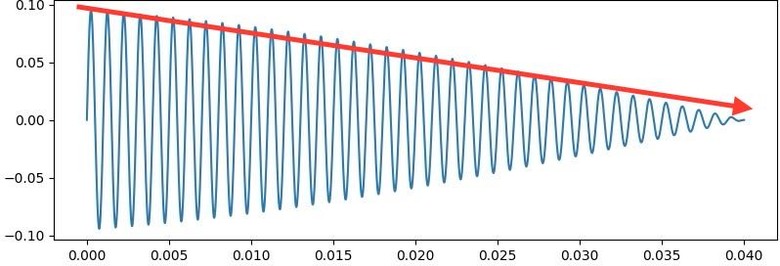
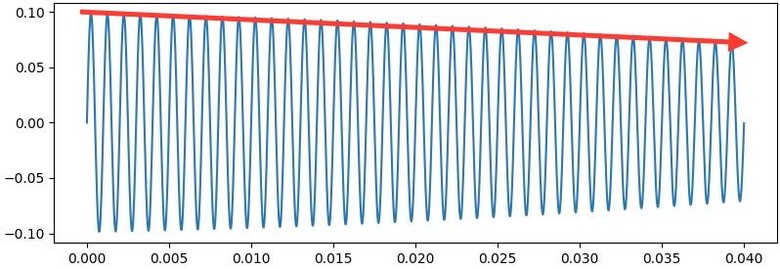
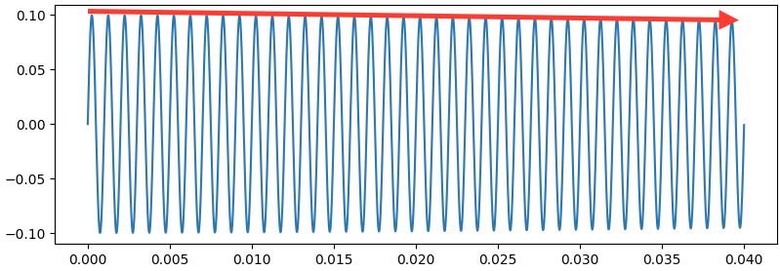
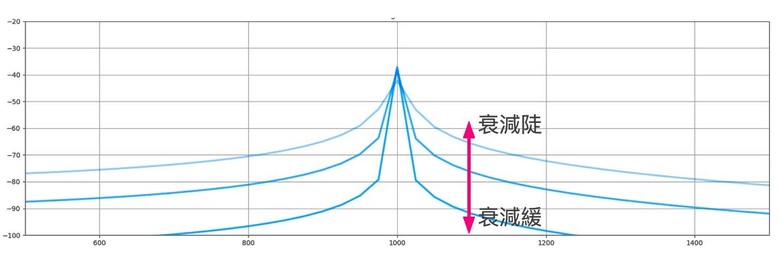
不同頻率的相異衰減時間 ...(恕刪)
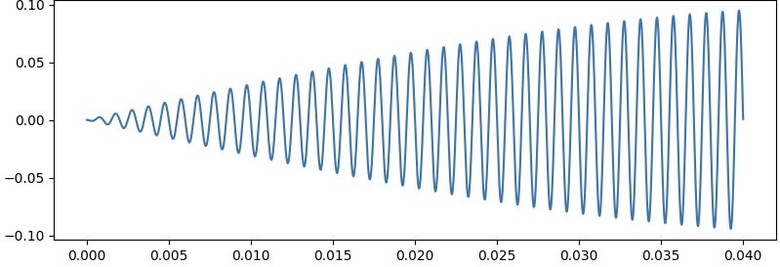
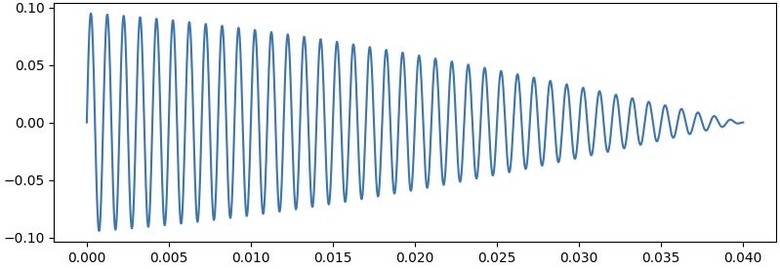
 「時間上的資訊藏在phase中」
「時間上的資訊藏在phase中」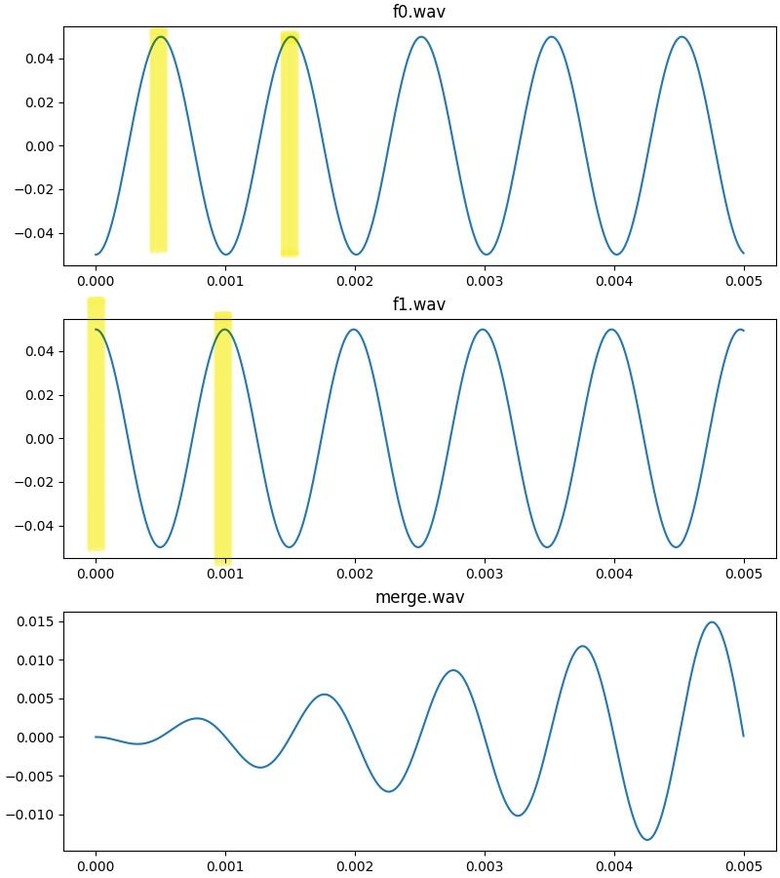
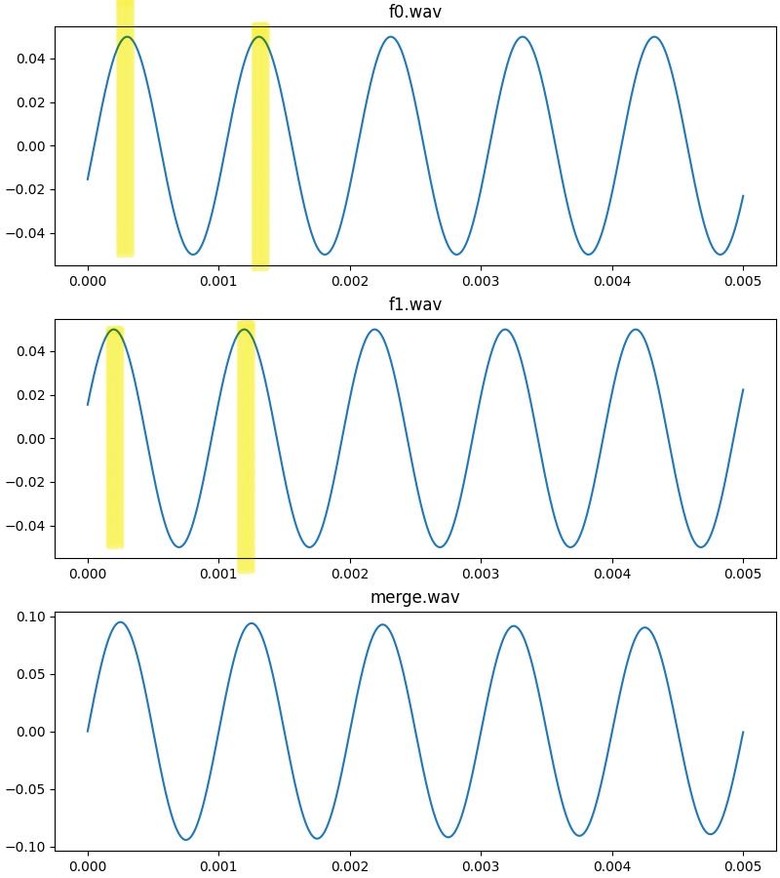
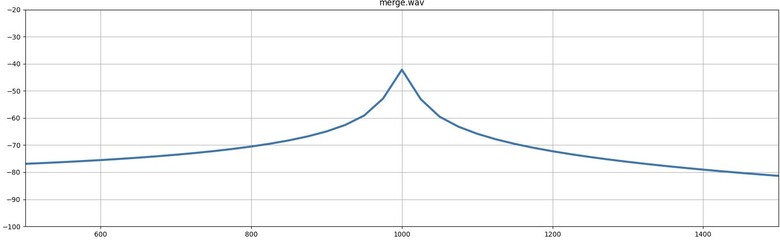


 !)
!)