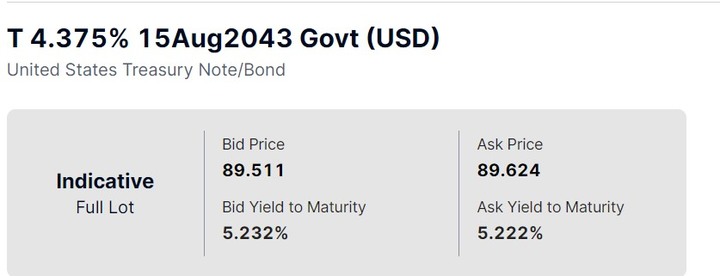
在台灣要直接購買T-bonds必須透過dealer,報價溢價、手續費和額度都不透明。
一般投資人在台灣要投資T-bonds,最簡單的方式就是透過ETF,但那是一籃子T-bond的組合,缺點就是無到期日,久期變動,殖利率(CY)扣掉交易及管理成本後不到5%。
如果你有美國劵商的帳戶就比較簡單,面額1000的公債,最小單位就是1K(一張),或是1K的倍數(n*K),市價就是劵商的報價,單位是面額的百分之多少成交。
例如下面這張成交單:

購買一張T-bond (面額1K),限價為面額的94.71%,成交價為面額的94.652744%
所以成交價為1000*94.652744=946.53元,劵商的手續費當交易1000張以下(1000*1000面額)時,為面額的0.2bp,但minimum是5元(當你買250張1000面額的T-bond以上才會超過),所以這張交易手續費就是最低手續費5元。
所以總共付出946.53 + 5 = 951.53元,也就是成本,所以YTM也有5.2%左右。
但海外劵商的缺點就是你的信任程度及美元交易的匯率風險,這就看個人喜好了!